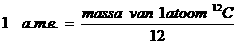kwantitatieve analyse

Inleiding

Inhoud

1. ATOOMMASSA

1. Hoe zit het ook weer met de massa van één elektron t.o.v. de kerndeeltjes?
2. Is er verschil tussen de massa van een atoom calcium en een ion calcium?

Isotopen

2. MOL

1. een micro-eenheid voor de zeer kleine deeltjes (atomen, moleculen, ionen, elektronen). Deze mikro-eenheid is een eenheid van massa: de UNIT (de atomaire massa-eenheid = a.m.e.)
2. een macro-eenheid voor zodanig grote aantallen kleine deeltjes dat ze te wegen zijn op een gewone weegschaal. Deze eenheid, MOL, is een eenheid van aantal.
   

   Eén MOL is 6.1023

   
   Opdracht 7
   Zet naast elkaar de volgende aantallen: één dozijn, één gros, één mol; leg uit dat het geen zin heeft om te spreken van één mol mensen.
   
   N.B.
   Let er op dat je het scheikundig begrip MOL niet verwart met het biologische begrip; het meervoud van mol is in de scheikunde molen. Ook moet je in je schrift of ergens anders het woord molecuul niet afkorten tot mol, want ook dat kan vergissingen veroorzaken.
   De schrijfwijze: (MOL en mol) worden allebei wel gebruikt.
   
   
   Omdat elektronen voor de massa niet meetellen zit de atoommassa dus geconcentreerd in de atoomkern. Als je dus het aantal kerndeeltjes van een atoom kent, dan ken je automatisch ook de massa van dat atoom in u(nits).
   Neem je dan vervolgens van die stof één mol (6.10²³) atomen, dat weet je daarvan de massa in grammen.
   
   Voorbeeld: Calcium (http://nl.wikipedia.org/wiki/Calcium)
   • Calcium (⁴⁰Ca)heeft 20 protonen en 20 neutronen; samen 40 a.m.e.
   • 1 atoom Ca weegt dus 40 u.
   • 6 x 10²³ atomen Ca wegen dus 6.10²³ x zoveel;
   • 1 mol calciumatomen wegen 6.10²³ x 40 u = 40 gram
   In de tabel vind je voor de atoommassa van Calcium het getal 40,1 (is dus een gevolg van isotopen).
   40 is het aantal kerndeeltjes van een normaal calciumisotoop met 40 nucleonen)
   Het getal 40,1 (atoommasse) op micro én op macronivo toepassen:
   • één atoom calcium weegt 40,1 u(nits){micronivo}
   • één mol calcium weegt 40,1 gram {macronivo}
   
   Opdracht 8
   Zink en koper samengesmolten levert messing op.
   zie: http://nl.wikipedia.org/wiki/Messing_(metaallegering)
   
   1. Leg uit hoeveel 1 mol zink + ½ mol koper samen (messing) wegen zowel op micro als op macronivo.
      Zorg er voor dat je de gegevens van tabel V op micro én op macronivo kan lezen.
   2. Hoeveel weegt: 1 mol suiker; ½ mol water; 10³ mol H₂
   
   
   
   

   2.1 Eenheden omrekenen.

   In de praktijk werk je vaak met de eenheden: (milli)gram, kilogram, ton, vooral als je met vaste stoffen werkt.
   Werk je met vloeistoffen en zeker als je met gassen werkt, dan zul je vaak volume-eenheden gebruiken: liters (=dm³), milliliters (ml = cm³), m³. Je moet in staat zijn met deze eenheden goed en snel te werken.
   Bestudeer onderstaand schema.
   
   
   
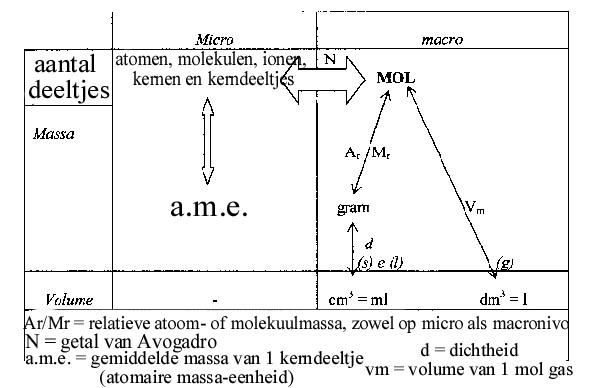
   Opdracht 9
   Hoeveel mg is 1 ton? hoeveel liter is 1 ml? Dit soort omrekeningen moet je snel en uit je hoofd kunnen doen!
   Geen gezeur hierover a.u.b., maar lekker oefenen.
   
   Je hebt bij natuurkunde geleerd hoe je voor vaste stoffen en vloeistoffen om kan rekenen van massa naar volume en omgekeerd. Daarbij maak je gebruik van de soortelijke massa, de dichtheid.
   De gebruikte eenheid in tabellen kan op drie manieren worden gelezen: ton/m³ = kg/l = gr/ml (boven en onder de streep worden steeds 1000 x zo klein.
   
   1 liter alkohol weegt dus 0,8 kg, maar ook:
   
   1 ml alkohol weegt 0,8 gram (= 800 mg).
   
   
   
   Opdracht 10
   Hoeveel weegt 10 liter benzine en hoeveel mol is 10 l benzine? (formule: C₈H₁₈(l); dichtheid=0,72)
   
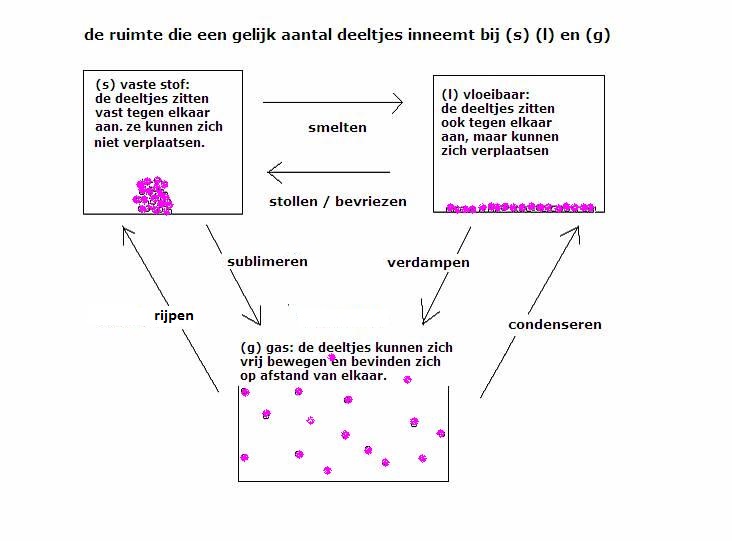
   Wil je voor een gas weten wat het volume is van één mol van dat gas, dan gaat de berekening heel anders.
   Er is een fundamenteel verschil tussen gassen enerzijds en vaste stoffen en vloeistoffen anderzijds: Het eigenaardige van gassen is dat alle gasdeeltjes los zijn van elkaar en dat daarom het volume van een gas niet afhangt van de grootte van de gasmoleculen.
   Het gaat er maar om hoe ver al die moleculen van elkaar af zitten. Hoe groot is de onderlinge afstand tussen die moleculen? Daar gaat het om.
   
   Bij vaste stoffen en vloeistoffen zitten of bewegen alle moleculen tegen elkaar aan. Dus bij (s) of (l) gaat het wel om de vraag: hoe groot zijn die moleculen? hoe groter, hoe meer volume ze innemen. Maar zo is het dus niet bij gassen!!
   
   Het volume van een gas, dus eigenlijk de onderlinge afstand tussen de gasmoleculen, wordt dan ook in de eerste plaats en vrijwel uitsluitend bepaald door druk en temperatuur:
   1. Bij hogere druk zitten de gasmoleculen dichter op elkaar en is de onderlinge afstand kleiner en krijg je méér moleculen per liter en dus ook meer mol per liter. Ook wordt daardoor het gas zwaarder.
   2. Bij hogere temperatuur (d.w.z. de deeltjes bewegen dan feller) gaan de gasmoleculen wat verder uit elkaar zitten. Je krijgt zo minder moleculen gas per liter en dus minder mol/l. Een liter warm gas is ook lichter dan een liter koud gas.
   Bij 0°C en 1 atm.druk is het volume van 1 mol gas 22,4 liter ongeacht welk gas het is. Bij een andere temperatuur en druk is dat volume anders, maar wel voor elk gas weer hetzelfde (dus: bij 100°C heeft elk gas een volume van bijv. 27 liter).
   
   M.b.v. de algemene gaswet kun je berekenen hoeveel liter een mol gas is bij bepaalde temperatuur en druk. We hebben daarvoor een wiskundige formule.
   
   Als je van twee gassen een gelijk volume neemt bij gelijke temperatuur en druk, dan bevinden zich daarin een gelijk aantal mol en een gelijk aantal moleculen, welk gas je ook neemt (zie fig).
   
   Bij het omrekenen van eenheden staat altijd bij de scheikundige berekeningen het begrip MOL centraal. Je moet het schema bij opdracht 19, over het omrekenen van eenheden uit je hoofd leren en snel toe kunnen passen.
   
   Opdracht 11
   Een auto verbruikt 1 l benzine op 15 km.
   Hoeveel mol benzine worden verbrand bij een rit van 200 km?
   
   Opdracht 12
   Hoeveel massa% C en H bevat aardgas?
   
   Opdracht 13
   Haal de nodige gevens uit onderstaande tabel die de oplosbaarheid geeft van een gas in water:
   
   

   	CO2	O2	NH3
   0°C	75·10-3 mol/l	2·10-3 mol/l	52 mol/l
   25°C	34·10-3 mol/l	1·10-3 mol/l	26 mol/l
   100°C	0,0·10-3 mol/l	0,7·10-3 mol/l	0,0

   
   Bereken m.b.v. de tabel hoeveel gram koolzuurgas er opgelost is in een halve liter verzadigde oplossing van 25°C.
   
   Opdracht 14
   Hoeveel water bevindt zich in 500 gram kristalsoda?
   
   Ook plastics, nylon, polyesters, polyethers e.d. zijn opgebouwd uit moleculen.
   De molecuulmassa's van deze moleculen variëren tussen 10.000 en 1000.000.
   We hebben dan te maken met zeer grote moleculen: MACROMOLECULEN
   
   Klassikaal wordt gedemonstreerd hoe je 0,1 M NaCl maakt en welke instrumenten er bij dit soort bezigheden gebruikt worden.
   Je moet in elk geval weten wat verstaan wordt onder de volgende begrippen:
   • weegschaal
   • pipet
   • maatkolf (zie ook http://nl.wikipedia.org/wiki/Maatkolf)
   • buret (zie ook http://nl.wikipedia.org/wiki/buret)
   • maatcylinder (zie ook http://nl.wikipedia.org/wiki/maatcylinder)
   • gasmeetspuit
   bestudeer ook onderstaande foto's van glaswerk:
   
   
   
   
   
   
   

   2.2 Elementenanalyse van koolstofverbindingen

   Een koolstofverbinding (organische chemie) bevat altijd C, vaak H en soms O.
   Andere elementen zoals N en S laten we hier buiten beschouwing. De formule van de te onderzoeken stof is bijvoorbeeld: C_xH_yO_z
   
   Bij de elementenanalyse bepaal je de hoeveelheid C en H in (milli)gram.
   Omdat je van te voren de massa van de totale stof hebt bepaald, kun je automatisch zien of er ook O in zat en zo ja, hoeveel.
   
   
   
   
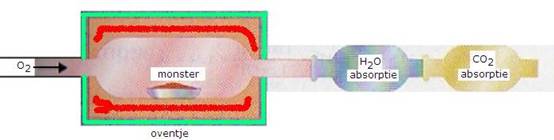
   1. Je weegt dus zeer zorgvuldig en nauwkeurig een bepaalde hoeveelheid van de te onderzoeken organische stof af (een monster).
      Vervolgens wordt deze stof met veel zuurstof volledig verbrand; alle C wordt omgezet in CO₂ en alle H in H₂O.
   2. De hoeveelheid koolzuurgas en water wordt gewogen.
   1. Uit de hoeveelheid koolzuurgas bereken je de hoeveelheid C.
   2. Uit de hoeveelheid water bereken je de hoeveelheid H.
   3. Nu kun je nagaan of in de oorspronkelijke stof ook nog O zat; zo ja, dan kun je die hoeveelheid O nu ook opschrijven.
      Als de oorspronkelijke hoeveelheid afgewogen stof méér is dan C + H samen, dan moet er dus ook O in zitten.
   
   Je kent nu de massaverhouding C : H (: O)
   Die massaverhouding moet je omzetten in de molverhouding door te delen door de bijbehorende atoommassa's van C, H (en O).
   Je krijgt op die manier de verhouding x : y : z
   
   Opdracht 15
   Leg uit dat je op deze manier slechts de verhoudingsformule (C_xH_yO_z)_n kan bepalen en niet de echte molecuulmassa C_xH_yO_z.
   
   Het koolzuurgas en het water dat bij de elementenanalyse moeten worden bepaald, kunnen als volgt worden opgevangen en gewogen:
   
   1. Eerst wordt het water(g) opgevangen door een hygroscopische stof die voor en na de proef wordt gewogen.
      Daarvoor kan bijvoorbeeld gebruikt worden: watervrij calciumchloride of watervrij kopersulfaat.
   2. Daarna wordt het koolzuurgas opgevangen bijvoorbeeld door een sterke base als kalk.
      Ook dat kalk wordt voor en na de proef gewogen. Het verschil is dan het opgenomen gas.
   
   Opdracht 16
   Iemand verbrandt 100 cc benzine met overmaat droge en zuivere zuurstof.
   De verbrandingsproducten worden achtereenvolgens geleid door watervrij calciumchloride en door kalk.
   Het kalkbuisje wordt 220 gram zwaarder en het calciumchloridebuisje wordt 102 gram zwaarder.
   Vervolgens wordt 10 cc benzine opgelost in 100 gram aceton; dit veroorzaakt een kookpunt van 57,40 °C.
   Bepaal de molecuulformule van deze benzine.
   
   
   
   

   3. CONCENTRATIE / MOLARITEIT

   Alle mengsels zijn samengesteld uit twee of meer komponenten. Als de komponenten niet van elkaar te onderscheiden zijn, spreekt men van een homogeen mengsel: alle deeltjes van het mengsel zijn zeer gelijkmatig over de hele ruimte verdeeld. Bij gasmengsels is dit altijd het geval, bijv. lucht.
   Als één van de komponenten (l) is en dit mengsel is helder (transparante), dan heb je een homogene oplossing; bijv. suikerwater. De vloeistofkomponent die de hele ruimte vult en die tevens het grootste deel van het mengsel is, noemt men het oplosmiddel; de andere komponent(en) is (zijn) de opgeloste stof(fen), die op zichzelf (s), (l) of (g) kunnen zijn.
   
   Als de deeltjes van een komponent niet gelijkmatig over de ruimte zijn verdeeld, dan spreekt men van een heterogeen mengsel.
   Voorbeelden: krijt in water, rook, olie + water, piepschuim.
   
   Alleen als de deeltjes van een komponent gelijkmatig over de ruimte verdeeld zijn (homogeen), kan men van die komponent een concentratie berekenen: elke liter van het oplosmiddel bevat dan evenveel moleculen van de opgeloste stof, waar je die liter ook weghaalt uit het mengsel.
   
   Opdracht 17
   Kun je de zoutconcentratie van zeewater bepalen? En de zandconcentratie in modder?
   Leg je antwoorden uit.
   
   Voor heterogeen verdeelde stoffen kan men dus geen concentratie berekenen.
   
   In de scheikunde neemt men als eenheid van concentratie meestal mol/liter = mol.l^-1
   Als men de concentratie van een stof in de formule wil aangeven wordt dat gedaan met vierkante haakjes: [NaCl]; [O₂]
   
   Een ander veelgebruikt woord voor mol/liter (concentratie) is molariteit. Een veel gebruikte afkorting bij de formules is .....M.
   Stel dat je een zoutzuuroplossing hebt met een concentratie van 0,4 mol HCl per liter water, dan zegt men wel: deze zoutzuuroplossing is 0,4 molair;
   de molariteit is 0,4 en men schrijft: 0,4M HCl.
   
   Opdracht 18
   Leg uit wat bedoeld wordt met: 10^-4M CO₂
   
   Als de concentratie van een oplossing bekend is én ook de hoeveelheid oplosmiddel, dan kun je berekenen hoeveel opgeloste stof er totaal in zit:
   
   10 ml 0,1M HCl bevat 0,01 x 0,1 mol HCl (10 ml=0,01 l)
   5 liter 0,02M NaCl bevat 5 x 0,02 mol NaCl
   
   Opdracht 19
   Bereken hoeveel gram suiker zit in één kopje (100 ml) 0,3M suikerwater.
   
   Bij concentratieberekeningen moet je altijd op minstens twee stoffen letten:
   1. de opgeloste stof wordt gegeven in molen.
   2. Het oplosmiddel wordt gegeven in liters.
   
   
   Bovendien moet je goed kunnen omrekenen van mol naar mmol, van liter naar ml en omgekeerd:
   1 ml = 10^-3 l
   1 l = 10³ ml
   1 mol/l = 10^-3 mol/ml
   
   Opdracht 20
   Vul in:
   1. 0,4M NH₃ = ....... mmol/l
   2. 10 ml 0,2 M NaCl bevat ..... mol NaCl
   
   Opdracht 21
   Een handelsoplossing van zoutzuur bevat 38% puur zoutzuur. De dichtheid is 1,2 g/ml. De molariteit is 12.
   Iemand koopt 100 kg van die handelsoplossing.
   Hoeveel HCl-moleculen heeft hij dan gekocht?
   
   Als ergens scheikundige analyse wordt gedaan blijkt dat de concentraties van vele onderzochte stoffen ver beneden de 1 M te liggen, bijvoorbeeld: 10^-3M 3.10^-9M enz.
   Om met zulke kleine concentraties snel en gemakkelijk te kunnen werken, maakt men in de scheikunde gebruik van de zgn. p-waarde. Wiskundig betekent dit: -log; Men laat het teken én het grondgetal 10 gewoon weg:
   
   p..... = 3 wil dus zeggen: [.....] = 10^-3 mol/liter
   
   Opdracht 22
   Wat betekent dus:
   1. pNaCl = 2
   2. pNH₃= 6
   
   Soms wordt ook de stof zelf verkort opgeschreven; ladingen worden weggelaten, soms nog meer:
   
   
   • pH = 5 betekent: [H₃O⁺] = 10^-5 mol/l
   • pOH = 7 betekent: [OH^-] = 10^-7 mol/liter
   Probeer nu de actie-opdracht A uit te voeren, te vinden aan het eind van deze module.
   
   
   
   

   4. BEPALING VAN MOLECUULMASSA

   Weet je dit nog?:
   • Micronivo: 1 molecuul van een stof weegt M u(nit).
   • Macronivo: 1 mol van een stof weegt M gram.
   • 1 u(nit) is de gemiddelde massa van één kerndeeltje.
   Het rechtstreeks wegen van 1 molecuul is onmogelijk, dus moet molecuulmassa M altijd indirect, via omwegen, worden bepaald.
   Eén mol afwegen kan wel, maar dan moet de molecuulmassa M al bekend zijn. Het gaat er nu om hoe je de molecuulmassa van een stof kan bepalen.
   
   De bepaling van M van een onbekende stof begint vaak met nauwkeurig afwegen van een bepaalde hoeveelheid grammen; daar doet men dan proeven mee.
   
   Opdracht 23
   Leg uit waarom het bij de bepaling van een molecuulmassa altijd om onbekende stoffen gaat; en verklaar waarom je die stof zuiver moet hebben.
   
   Voor een goed experiment is nodig dat de te onderzoeken stof homogeen binnen een bepaalde ruimte is verdeeld.
   De methode die men toepast is afhankelijk van de toestand van de stof:
   1. methode I passen we toe als de stof vast of vloeibaar is.
   2. methode II passen we toe als de stof een gas is.
   
   Als de stof (s) of (l) is, moeten de moleculen homogeen verdeeld worden.
   Daartoe wordt die stof...:
   1. opgelost in een geschikt oplosmiddel; van het mengsel (de oplossing) bepaal je vervolgens het vriespunt of het kookpunt.
      (dit is Methode I)
   2. verdampt. (dit is Methode II)
   
   
   

   4.1 Methode I:

   Opgeloste stoffen beïnvloeden het vriespunt en het kookpunt van een oplosmiddel; een vloeistof kookt en bevriest moeilijker als er vreemde deeltjes in de vloeistof aanwezig zijn.
   
   Opdracht 24
   Noem twee voorbeelden van vriespuntsbeïnvloeding in de winterse praktijk van het dagelijks leven.
   
   
   1. Bij bevriezen moet altijd een rooster worden gemaakt (bijvoorbeeld een ionrooster).
      De vorming van een rooster wordt bemoeilijkt als er vreemde, dus niet in het rooster passende deeltjes aanwezig zijn, dus als er een stof is opgelost. De roostervorming wordt verstoord.
      Om toch een rooster te vormen is dan een lagere temperatuur nodig: VRIESPUNTSVERLAGING (v.p.v. of v.p.d.)
   2. Bij koken van een vloeistof moeten de moleculen aan het oppervlak uit die vloeistof kunnen ontsnappen.
      Als er vreemde deeltjes van een opgeloste stof aanwezig zijn, dan nemen die een deel van het totale oppervlak in bezit.
      Het wordt dan moeilijker voor de oplosmiddelmoleculen om uit die vloeistof te ontsnappen: k.p.v. = KOOKPUNTSVERHOGING.
   
   Deze effekten (v.p.v. en k.p.v.) zijn niet zozeer afhankelijk van de aard van de opgeloste deeltjes, dus het is niet belangrijk wat voor deeltjes het zijn (bijv. ionen, atomen, grote of kleine moleculen), maar vooral van de hoeveelheid opgeloste deeltjes (het aantal mol dus).
   
   Opmerkelijk is dat men bij deze bepalingen niet de gebruikelijk eenheid mol/liter gebruikt, maar mol/100 gr oplosmiddel. Vraag me niet waarom; het is zo gegroeid.
   De hoeveelheid onbekende stof die je afweegt (bijv. p gram) wordt opgelost in een afgewogen hoeveelheid bekend oplosmiddel (bijv q gram).
   Als je dan het vriespunt of het kookpunt van het mengsel meet (bijvoorbeeld met een zeer nauwkeurige Beckmannthermometer), én je kent het vriespunt/kookpunt van het zuivere oplosmiddel, dan ken je v.p.v. of k.p.v.
   De (onbekende) molecuulmassa van de opgeloste stof noemen we M.
   Het aantal opgeloste deeltjes is p/M. Dit aantal mol deeltjes bepaalt dus de verhoging of de verlaging.
   
   Opdracht 25
   Stel dat je de M hebt gevonden nl. 58,44 u en bovendien weet je dat de stof uit ionen is opgebouwd, welke stof zou het dan kunnen zijn?
   En aan welke bijzonderheid moet je dan denken bij het vaststellen van het aantal mol deeltjes?
   
   
   Het aantal opgeloste deeltjes is dus p/M. Dit aantal mol deeltjes bepaalt de verhoging of de verlaging.
   Het aantal mol opgeloste stof is evenredig met de v.p.v. of k.p.v.
   
   v.p.v./k.p.v. ≡ aantal mol opgeloste stof
   
   De hoeveelheid oplosmiddel zal in de praktijk zeker niet altijd precies 100 gram zijn; neem je minder, dan is het effect sterker, neem je meer oplosmiddel (de boel is dan sterker verdund), dan is het effect minder.
   Stel dat je q gram neemt, dan is voor het oplosmiddel een korrektiefaktor nodig: 100/q
   
   v.p.v. 0f k.p.v. ≡ aantal mol opgeloste stof x 100/q
   
   Om van een evenredigheidsteken over te stappen op een = teken, moet een constante worden ingevoerd die we aanduiden met K*.
   Deze constante K* heet de molaire k.p.v./v.p.v.
   De waarde van K* is per oplosmiddel verschillend en kun je vinden in tabellen.
   
   Opdracht 26
   de molaire k.p.v van water is 0,5; van benzeen 2,5
   de molaire v.p.d. van water is 1,9; van benzeen 5
   1. Bij welke temperatuur bevriest water als er 1 mol stof in opgelost wordt per 100 gr water?
   2. Idem voor het oplosmiddel benzeen.
   
   Als een stof uit ionen is opgebouwd, dan splitst die stof bij oplossen in water in meerdere deeltjes (n deeltjes)
   
   v.p.v. of k.p.v. = K* x aantal mol opgeloste stof x 100/q · n
   
   of:
   
   v.p.v. of k.p.v. = K* · p · 100 · n
                                      M · q
   
   Opdracht 27
   25 gram stearinezuur wordt opgelost in 100 gram alkohol.
   Bepaal (als de apparatuur er is) het kookpunt en dus de k.p.v. en bepaal de molecuulmassa van stearinezuur.
   
   Opdracht 28
   Een mengsel van 5,14 mg van stof Y en 251 mg fenol heeft een vriespunt van 38,53^oC.
   Bereken de molecuulmassa van stof Y.
   
   Opdracht 29
   5 gram van een zout wordt opgelost in 50 ml water.
   
   1. Bepaal (als de apparatuur er is) het vriespunt van dit mengsel en dus de v.p.v.
   
   
   2. Bereken de molecuulmassa van het zout.
   
   
   
   

   4.2 Methode II

   Indien de stof (g) is, heb je per definitie met een homogene stof te maken; een gas is altijd homogeen over de ruimte verdeeld.
   Ook hier wordt eerst gewogen: een bepaald volume gas wordt gewogen bij bekende temperatuur en druk.
   
   Opdracht 30
   Leg uit of zoek uit hoe je een gas kunt wegen.
   
   Vervolgens weeg je eenzelfde hoeveelheid waterstofgas bij gelijke temperatuur en druk. Je kunt dan uitrekenen hoeveel keer zo zwaar het onbekende gas is als waterstofgas.
   
   Opdracht 31
   Leg uit waarom de gassen X (het onbekende gas) en H₂ bij gelijke temperatuur en druk worden gewogen.
   
   Als je weet dat het gas, waarvan je de M wil bepalen, x keer zo zwaar is als waterstofgas dan noemen we dat getal x: de dampdichtheid D_H.
   
   

   Definitie: DH =    massa van V liter gas (bij t en p)             massa van V liter H2 (bij t en p)

   
   
   Als je bedenkt dat voor gassen bij gelijke t en p altijd geldt dat in een gelijk volume een gelijk aantal moleculen zitten, dan kun je uit die definitie de volgende formule afleiden:
   
   D_H = M(gas)/M(H₂)
   
   of liever:
   
   

   M = 2DH

   
   
   Opdracht 32
   Leid deze formule af uit de definitie.
   
   Opdracht 33
   Je onderzoekt een onbekende stof X(s).
   Als je stof X in zoutzuur oplost, ontstaat er een gas A.
   Eén liter van dat gas A wordt gewogen: 1,98 gram.
   Een gelijke hoeveelheid waterstof bij dezelfde t en p weegt 0,09 gram.
   Vervolgens neem je 10,6 gram van stof X en lost die op in 400 ml water.
   Het vriespunt wordt gemeten en blijkt -1,4°C te zijn.
   Probeer er achter te komen wat stof X is.
   
   
   
   

   5. REACTIEBEREKENINGEN

   (zie ook module 07)
   Toen lang geleden Jules Verne zijn fantastische reis naar de maan beschreef, somde hij precies op hoeveel kruit er nodig was om de "raketkogel" met de bemanning de nodige kracht te geven om de aarde te kunnen verlaten, hoeveel stoffen er mee genomen moesten worden om daaruit precies de benodigde hoeveelheid zuurstof te maken die de bemanning voor het geplande aantal dagen nodig zou hebben, enzovoort.
   Als tegenwoordig zoiets gebeurt dan worden dergelijke berekeningen nog steeds met dezelfde nauwkeurigheid of beter, gedaan.
   Bijvoorbeeld: Een vaste raketbrandstof is hydrazine dat gemaakt kan worden door nauwkeurig afgepaste hoeveelheden ammoniak (in liters gas) en natriumhypo(=onder)chloriet (in grammen) samen te laten reageren tot de gewenste hoeveelheid hydrazine.
   
   Opdracht 34
   Iemand wil een zeepfabriek opzetten. Nodig voor het proces zijn: plantaardige olie, keukenzout, natriumhydroxide, water, energie, gebouwen, enzovoort.
   Geef een kort overzicht van het directieplan.
   
   Ander voorbeeld:
   Als in een zwavelzuurfabriek zwaveldioxide(g), zuurstof(g) en water(l) gemengd worden om zwavelzuur te maken, dan wordt heel precies berekend hoeveel van elke reactant nodig is.
   
   Zo zijn er talloze toepassingen te noemen waarbij een bedrijf of een andere instelling op grond van goed kloppende reactievergelijkingen moet gaan berekenen hoeveel product er gemaakt kan worden uit hoeveel reactant.
   Als je dit niet doet en je gooit maar willekeurig wat bij elkaar, dan is ten eerste de kans groot dat er heel verkeerde (bij)producten ontstaan en ten tweede gaat er veel reactant verloren; economisch gezien zou het gewoon handenvol geld kosten.
   Een goede bedrijfsvoering vraagt dus om iemand die verstand heeft van reactieberekeningen.
   
   
   

   5.1 Algemeen

   
   Demonstratie op school, of in een lab:
   x gr magnesium wordt opgelost in voldoende 1M HCl.
   Het gas dat daarbij ontstaat wordt opgevangen en gemeten in een gasmeetspuit.
   Met die bekende hoeveelheid gas, gemeten bij kamertemperatuur moet berekend worden hoeveel magnesium in het zoutzuur werd opgelost.
   
   Als je chemische reacties laat verlopen, is het belangrijk dat je weet hoeveel van de reactanten nodig is en hoeveel van de producten er kan ontstaan. Dit is zowel chemisch alsook economisch van groot belang.
   
   Het zijn altijd atomen, moleculen of ionen die bij botsing met elkaar reageren; deze deeltjes kunnen heel verschillend zijn in grootte en in massa (hoeft niet!).
   Zo kan bijvoorbeeld een groot en zwaar atoom heel goed reageren met een heel klein ion. Uiteraard heeft dat dan gevolgen voor de massaverhouding.
   
   Voor elke reactie ligt wél vast: hoeveel atomen, moleculen of ionen, dus in welke verhouding ze met elkaar zullen reageren. Dit vaste aantal is af te lezen aan de coëfficiënten van een kloppende reactievergelijking.
   Die coëfficiënten in de reactievergelijking hebben twee betekenissen:
   • de microbetekenis: aantal ionen, atomen e.d.
   • de macrobetekenis: aantal mol
   In de reactie: 2H₂ + O₂ 2H₂O betekenen de coëfficiënten:
   1. (micro): 2 moleculen waterstof reageren met 1 molecuul zuurstof en levert op 2 moleculen water.
   2. (macro): 2 mol waterstof reageert met 1 mol zuurstof en levert op 2 mol water.
   De verhouding 2 : 1 : 2 ligt vast voor deze reactie en heet de molverhouding.
   Een reactieberekening begint dus altijd met een goede reactievergelijking.
   
   Opdracht 35
   Laat zien in welke molverhouding calcium en water met elkaar reageren en bereken in welke massaverhouding deze stoffen dus reageren.
   
   Let er op dat een reactie zelf de coëfficiënten bepaalt. De coëfficiënten zijn niet afhankelijk van de hoeveelheid stoffen die je samenvoegt.
   Zelfs al voeg je 100 mol waterstof bij 1 mol stikstof, dan zal toch de molverhouding van de reactie dezelfde blijven:
   
   N₂(g) + 3H₂(g) 2NH₃(g)
   dus
   1 : 3 : 2
   
   Opdracht 36
   Leg uit dat in bovenstaand voorbeeld niet meer dan 2 mol ammoniak kan ontstaan.
   
   Stoffen die uit ionen zijn opgebouwd (meestal te herkennen aan het feit dat er een metaal in de verbinding zit) zijn in opgeloste vorm in ionen gesplitst; in vaste vorm hebben deze stoffen een ionrooster.
   Bij reactieberekeningen gaat het meestal om de hoeveelheden ongesplitste stof, die nodig zijn of die ontstaan. Daarom schrijft men bij dit soort berekeningen de formules van die stoffen liever niet in ionen; dit vergemakkelijkt het rekenen.
   Je weegt immers ook de hele stof af en niet slechts één ionsoort; een potje met alleen natriumionen bestaat niet.
   
   
   Wel in ionen: Na⁺ + Cl^- + Ag⁺ + NO₃^- Na⁺ + NO₃^- + AgCl(s)
   
   Niet in ionen: NaCl(aq) + AgNO₃(aq) NaNO₃(aq) + AgCl(s)
   
   Bij berekeningen heeft dus de laatste schrijfwijze de voorkeur.
   Noteer ook altijd de aggregatietoestand (de fase):(s) (l) (g) (aq). Dit voorkomt veel fouten.
   
   De reactanten reageren dus in een vaste molverhouding; als die reactanten niet in deze juiste molverhouding worden samengevoegd reageren ze net zo lang tot één van de reactanten op is.
   De rest blijft gewoon over zonder te reageren.
   
   Opdracht 37
   Stel dat je 1 g natrium verbrandt in 100 liter lucht.
   Bereken dan hoeveel g product er ontstaat en hoeveel liter zuurstofgas er overblijft. (0ºC, 1 atm.)
   
   Voor gassen en voor vloeistoffen gebruik je vaak een volume-eenheid: liters of mls.
   Bij de berekening moet je er goed aan denken dat het volume van een vloeistof meestal wordt omgerekend via de soortelijke massa of dichtheid en dat het volume van een gas meestal direct omgezet kan worden in het aantal molen (als je de temperatuur en de druk van het gas kent).
   
   Opdracht 38
   Bereken hoeveel liter waterstofgas er ontstaat als 10 gr calcium wordt opgelost in voldoende water.
   Het gas wordt gemeten bij 0ºC en 1 atm.
   
   Het is verstandig - voor een goed begrip van de praktijk - om aan te geven of de stoffen (s), (l) of (g) zijn (of (aq)):
   
   Ca_(s) + 2H₂O_(l) Ca(OH)_2(aq) + H_2(g)
   
   Deze berekening is ook een voorbeeld om het voordeel te zien van het gebruik van empirische formules boven ionformules.
   Chemische berekeningen gaan over praktische dingen en in de praktijk haal je geen ionen uit een fles, maar neutrale stoffen in hun geheel.
   Dus ook al doet alleen een Chloride-ion mee, toch weeg je keukenzout af (NaCl).
   
   N.B. Ken je de volgende vergelijking nog: d = g/v?
   
   Gassen hebben ook een dichtheid, maar met een volkomen andere definitie dan de dichtheid van (s) en (l).
   Alvast goed om iets te weten over gassen:
   wat voor gas je ook neemt, met grote of kleine moleculen, één mol ervan heeft altijd hetzelfde volume, gemeten bij dezelfde temperatuur en druk.
   Of anders gezegd:
   als je 1 liter neemt van een gas, gemeten bij een vaste temperatuur en druk, is dat bij elk gas een gelijk aantal mol.
   Mol en volume zijn bij gassen dus evenredig.
   Wat bij vaste en vloeibare stoffen echt niet opgaat, geldt wel voor gassen: de coëfficiënten van gassen in een vergelijking kunnen zowel gelezen worden als mol én als liters.
   
   Bij gassen geldt: MOLVERHOUDING = VOLUMEVERHOUDING
   
   Opdracht 39
   Welk volume heeft 1 mol gas bij een druk van 1 atm. en een temperatuur van 0ºC?
   
   Als methaan reageert met zuurstof in de verhouding 1:2 (één mol methaan reageert met 2 mol zuurstof), betekent dit tegelijk en automatisch dat, onder gelijke omstandigheden gemeten, 1 liter methaangas reageert met 2 liter zuurstofgas.
   
   
   Reactieberekeningen kunnen meestal worden aangepakt met behulp van onderstaand werkschema:

   Een kloppende reactievergelijking opstellen en de aggregatietoestanden aangeven. Onderstreep de stoffen waarover gegevens bestaan en waarover vragen gesteld worden. De andere stoffen hoef je niet mee te nemen. Die gegevens worden soms direct, soms indirect gegeven. De berekening doe je alleen met de onderstreepte stoffen. Noteer de molverhouding. Als je kans ziet om een proef ook echt uit te voeren, dan doe je dat het beste Waar nodig zet je mol om in de juiste eenheden (zie gegevens en het gevraagde) Voer een omrekeningsfactor in om recht te doen aan de werkelijke hoeveelheden, zoals blijkt uit de gegevens.Zo beëindig je de berekening. Controleer / Schat of de uitkomst reëel is, of zo'n uitkomst in werkelijkheid zou kunnen.

   Voorbeeldopdracht:
   Wat is de massa en het volume (standaardomstandigheden) van koolstofdioxide dat gevormd wordt bij de volledige verbranding van 4,01 g methaan?

   1	CH4(g) + 2 O2(g) CO2(g) + 2H2O(g)
   2	Onderstreep die stoffen waarover je gegevens hebt of waarover iets wordt gevraagd. CH4(g) + 2 O2(g) CO2(g) + 2H2O(g)
   3	Dus, 1 mol CH4(g) reageert met 1 mol CO2(g) (verhouding is 1:1)
   4	16 gram CH4(g) produceren 44 gram CO2(g) (hier passen we de molecuulmassa's toe)
   5	in werkelijkheid hebben we niet 16 gram, maar slechts 4 gram voor de verbranding. De in te voeren factor is dan: 4/16. 4/16 x 16 gram CH4(g) produceren 4/16 x 44 gram CO2(g) tenslotte: standaardomstandigheden wil zeggen: bij temperatuur van 25°C en druk van 1 atm. Dan is 1 mol gas = 22,4 liter 1/16 x 44 = 11 gram CO2(g) wordt geproduceerd, dat is gelijk aan 4/16 mol = 4/16 x 22,4 liter CO2(g) = 5,6 liter
   6	als je 4 g methaangas verbrandt, krijg je dus 5,6 liter kooldioxidegas. Zo op het eerste gezicht moet dat kunnen; het lijkt geen absurd antwoord

   
   
   Opdracht 40
   1 gram Natrium wordt verbrand in 100 liter lucht(0°C en 1 atm.).
   Bereken, in grammen, hoeveel zuurstof overblijft.
   
   Opdracht 41
   Een ijzererts bevat 75% ijzer(III)oxide. Bereken de massa van het ijzer dat verkregen kan worden uit 1 ton van dit erts.
   
   Opdracht 42
   Iemand gebruikt aardgas (methaan) om 5 liter water gedurende 15 minuten te koken, om eventuele bacteriën te doden.
   Daarbij gebruikte ze 5 gram gas.
   Bereken de massa, in grammen, van het benodigde zuurstof voor dit hele proces.
   
   Opdracht 43
   Om 1,3 mol aardgas te verbranden, hoeveel mol zuurstof zijn daarvoor nodig? (alles gemeten bij gelijke temperatuur en druk).
   
   Opdracht 44
   Bereken de hoeveelheid ammoniak en zuurstof (in grammen) die nodig zijn om 3,00 g NO te maken. Een bijproduct is water.
   
   Opdracht 45
   Geconcentreerd zwavelzuur bevat 96% puur H₂SO₄. De resterende 4% is water.
   Bereken het aantal mol H₂SO₄ in één liter geconcentreerd zwavelzuur, als je weet dat de dichtheid daarvan 1,84 g/cm³ is.
   
   Opdracht 46
   3 mol chloor en 150 gram ijzer reageren met elkaar en vormen ijzer(III)chloride.
   Welke stof is de beperkende stof (gaat helemaal op?): chloor of ijzer?
   
   Opdracht 47
   Stikstof en Waterstof reageren in een directe reactie met elkaar en vormen het product ammoniak, in een industriele reactor met katalysator.
   Er vormen zich 1000 gram product (ammoniak) met een rendement van 97,8%
   De molecuulmassa van ammoniak = 17,0
   Hoeveel mol reagens zijn nodig.
   
   
   

   5.2 Titraties

   
   
   
   
   
   In de klas wordt dit onderwerp meestal gestart door een demonstratie en bespreking van een eenvoudige zuurbasetitratie + berekening.
   Je zou het als volgt kunnen doen:
   1. Eerst wordt die titratie uitgevoerd m.b.v. een pH-meter en een schrijver, waarbij de titreervloeistof in een constant tempo wordt toegedruppeld uit de buret en wel tot ruim voorbij het eindpunt.
   2. Vervolgens wordt de titratie gedaan m.b.v. een indikator om precies in het eindpunt te stoppen.
   3. Tenslotte wordt de bijbehorende berekening uitgevoerd en besproken.
   Zie voor een aardige inleidende beschrijving ook: Titraties op wikipedia
   
   Opdracht 48
   25 ml kaliloog met onbekende concentratie wordt getitreerd met 16 ml 0,27M zoutzuur.
   Bereken de [KOH].
   
   Een titratie is een vrij snelle methode om concentraties van opgeloste stoffen te bepalen.
   Daarbij maken we graag gebruik van apparatuur waarop volumes van vloeistoffen nauwkeurig af te lezen zijn, zoals: pipetten, maatkolven en buretten.
   Je spreekt daarom ook van volumetrie.
   
   Aan een reactievergelijking kun je zien in welke molverhouding de reactanten met elkaar moeten reageren.
   Als de reactanten precies in dié molverhouding worden samengevoegd, spreekt men van equivalente hoeveelheden.
   
   Opdracht 49
   Bereken de equivalente hoeveelheid NaOH voor 0,3 mol zwavelzuur.
   
   Meestal laat men bij een titratie twee opgeloste stoffen voorzichtig met elkaar reageren en stopt men de reactie meteen op het moment dat equivalente hoeveelheden van de stoffen zijn samengevoegd.
   
   Opdracht 50
   10 ml tri-jodideoplossing (I₃^-) wordt getitreerd met 23,9 ml 0,1M thiosulfaat(S₂O₃^2-).
   Hoeveel gram jodium (I₂) bevatte de oorspronkelijke oplossing per liter?
   
   De concentratie van de titreervloeistof (meestal in de buret) moet nauwkeurig bekend zijn.
   De concentratie van de andere stoffen kan daaruit dan berekend worden.
   
   Op het moment dat equivalente hoeveelheden stoffen zijn samengevoegd moet je de reactie stoppen, dus ophouden met toevoegen uit de buret.
   
   Meestal stopt men de reactie iets te laat; met de laatste druppel titreervloeistof wordt iets teveel toegevoegd.
   Het praktische eindpunt van de titratie valt dan dus niet voor 100% samen met het theorethische equivalentiepunt. Je voegt dus automatisch iets te veel toe.
   Voor een betrouwbare bepaling mag de fout niet groter zijn dan 0,5%. In de praktijk betekent dit dat je hoogstens één druppel teveel mag toevoegen op 200 druppels.
   
   Opdracht 51
   Bij een titratie was 3 ml titreervloeistof (uit de buret) nodig (= ± 60 druppels); stel dat je een halve druppel teveel toevoegt, is je titratie dan nauwkeurig genoeg?
   
   
   

   Om het omslagpunt te kunnen waarnemen, is meestal een indicator nodig
   Bij een zuurbasetitratie:	een zuurbase-indicator
   Bij een redoxtitratie:	een redox-indicator

   
   
   Een indicator is meestal....:

   een zwak organisch zuur	een zwakke organische reduktor
   HIn H+ + In-	RedIn n e- + OxIn
   HIn andere kleur dan In-	RedIn andere kleur dan OxIn
   De kleur van het HIn of In-	De kleur van RedIn of OxIn
   is pas duidelijk te zien als het evenwicht voldoende links of rechts ligt.
   De kleur die een indicator aanneemt hangt af van de omgeving: In een zuur milieu(of in een reducerend milieu) liggen bovenstaande evenwichten naar links en overheerst dus de kleur van het HIn (of RedIn). Per indicator kan dit sterk verschillen.

   
   
   
   
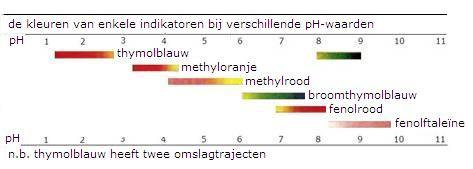
   Voor gegevens over nog meer indicatoren moet je tabel VIII opvragen.
   
   Opdracht 52
   Leg uit welke kleur fenolrood heeft in kaliloog; is het indicatormolecuul dan neutraal of negatief?
   
   Opdracht 53
   Leg uit welke kleur methyleenblauw heeft in een oplossing van natriumsulfiet; heeft het indicatormolecuul dan de Red- of de Ox-vorm?
   
   Bij zuurbasetitraties hoeft de pH van de eindoplossing niet altijd 7 te zijn; de eind-pH is namelijk afhankelijk van de eigenschappen van de producten.
   Deze producten kunnen op hun beurt weer zwakke zuren of basen bevatten.
   
   De volgende vuistregels kunnen worden toegepast:
   
   

   titratie van sterk zuur met sterke base:	pH = 7
   titratie van sterk zuur met zwakke base:	pH < 7
   titratie van zwakzuur met sterke base:	pH > 7

   
   
   Opdracht 54
   Leg uit waarom bij de titratie van azijnzuur met loog de eind-pH > 7 is.
   
   De juiste indicatorkeuze hangt af van de eigenschappen van de producten én van het omslagtraject van de indicator(tabel VIII).
   Je moet de indicator en de titratie op elkaar afstemmen.
   
   Opdracht 55
   Leg uit of methyloranje geschikt is als indicator voor de titratie van azijnzuur met loog.
   
   
   

   indirecte titraties

   Soms is het niet mogelijk de concentraties van een bepaalde stof direct door titratie te bepalen; bijvoorbeeld als zo'n stof gasvormig is, onstabiel of slecht oplosbaar.
   In zulke gevallen voert men een zgn. indirecte of terugtitratie uit.
   De stof waar het dan eigenlijk om gaat moet je van te voren al laten reageren met iets anders, een vervangende stof. De stof waar het om gaat doet dan aan de eigenlijke titratie niet mee.
   De vervangende stof wordt wél getitreerd en het aantal mol daarvan moet je uitrekenen.
   Daarna kun je, door terug te rekenen, toch bepalen hoeveel van die oorspronkelijke stof aanwezig was.
   
   voorbeeld:
   Marmer bevat een hoog gehalte aan calciumcarbonaat en dat gehalte wil je bepalen.
   Je zou een stof kunnen toevoegen die alleen met het calciumcarbonaat reageert en zo dat carbonaat verwijderen.
   Stel dat je daarvoor Salpeterzuur gebruikt; je moet er dan wel voor zorgen dat je heel nauwkeurig weet hoeveel salpeterzuur je in het begin hebt toegevoegd. Een deel van dat zuur reageert dan met het carbonaat en de rest blijft over.
   Als je dus precies weet hoeveel salpeterzuur je oorspronkelijk hebt toegevoegd en ook precies hoeveel je over hebt, dan is het verschil precies die hoeveelheid salpeterzuur die met het carbonaat heeft gereageerd.
   De rest, dus die hoeveelheid die overbleef, die bepaal je door titratie, bijvoorbeeld met Natronloog.
   
   Opdracht 56
   Je weegt precies 10 gram marmer af en brengt dit in 150 ml 1M salpeterzuur. Het gas dat daarbij ontstaat wordt door verwarming verwijderd.
   Daarna titreer je de rest salpeterzuur met 10 ml 0,2M natronloog.
   Bereken het gehalte aan calciumcarbonaat in het marmer.
   
   Een veelgebruikte redoxtitratie is een titratie met het koppel: I₃/S₂O₃^2-(jodium met thio).
   Deze titratie wordt meestal toegepast bij een indirecte titratie waarbij de te onderzoeken stof vervangen wordt door jodium of door thio, afhankelijk van de vraag of die onbekende stof een reduktor dan wel een oxidator is.
   Bij deze zogenaamde jodometrische titraties maakt men gebruik van de goedkope en goedwerkende indicator: zetmeel(aq), een stijfseloplossing.
   Vers zetmeel heeft spiraalvormige moleculen (zie ook module 12, biochemie) waarin de tri-jodideionen precies passen en zorgen voor een donkerblauwe kleur.
   Het tri-jodide zelf heeft ook een kleur (geelbruin), maar het verdwijnen of ontstaan daarvan is veel minder duidelijk waar te nemen dan die donkerblauwe kleur.
   
   Opdracht 57
   Schrijf op wat je kunt zien als je een jodiumoplossing titreert met thio en je gebruikt wel/geen stijfsel als indicator.
   
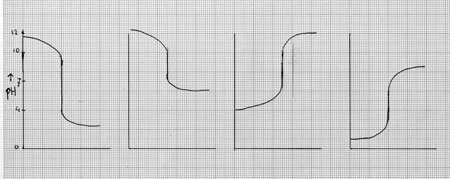
   Als je een zuurbasetitratie wil uitvoeren zonder indicator, dan kun je een pH-meter gebruiken en op die meter gedurende de titratie voortdurend het pH-verloop aflezen: in het equivalentiepunt is de pH-verandering het grootst, een plotselinge pH-sprong treedt op.
   Van het verloop van die pH kun je eventueel m.b.v. een plotter een grafiek laten maken (zie hieronder een voorbeeld).
   
   Steeds na toevoeging van bijv. 0,5 ml lees je de waarde van de zuurtegraad of van de potentiaal af op de meter en noteert die; je kunt dan zelf op grafiekenpapier een titratiekromme tekenen (of de plotter doet dat automaisch) en daaruit de plaats van het equivalentiepunt afleiden.
   
   Ook voor redoxtitraties is iets dergelijks mogelijk, maar dan gebruik je geen pH-meter, maar een potentiaalmeter.
   
   Opdracht 58
   Welke eindpuntsbepaling is volgens jou nauwkeuriger: met indicatoren of met afleesbare meters.
   
   Opdracht 59
   Wat voor zuurbasetitraties horen bij de vier titratiekrommen?
   
   
   Er zijn vele titratiemethoden die deels al besproken zijn of die later nog behandeld zullen worden in een aanvulling van deze module.
   Hieronder worden enkele genoemd:
   • neerslagtitraties
   • colorimetrische titraties
   • zuurbasetitraties
   • redoxtitraties
   • complexometrische titraties
   • coulometrische titraties
   • thermometrische titraties
   
   
   
   
   

   6. Werken met p-waarden en belangrijke constanten

   In diverse modules is al gewerkt met logarithmen, negatieve logarithmen en p-waarden.
   Het beste is om dat nu nog even op te halen door er mee te oefenen:
   • log10^-2 = -2 en ook:p10^-2 = 2
   • log 4.10^-2 = log4 + log10^-2 = -2 + log4 = -2 + 0,60= -1,40 en ook:p4.10^-2 = p4 + p10^-2 = 2-log4= 2-0,60 = 1,40
   • pX = 3,7 = 4-0,3 = 4-log2,00 dus ook: X = 2.10^-4
   
   
   
   

   6.1 pH

   De reden dat men veel met negatieve logarithmen (p-waarden) werkt ligt in het gegeven dat in de scheikunde de concentraties van stoffen zo klein is.
   Als je er eenmaal aan gewend bent, zul je merken dat het veel eenvoudiger is om te schrijven:
   
   pH = 6 i.p.v. [H₃O⁺] = 10^-6 mol/l
   
   of:
   
   pOH = 8 i.p.v. [OH^-]= 10^-8 mol/l
   
   Altijd als je de concentraties opschrijft, moet je de eenheid mol/l er bij zetten. Als je met de p-waarde werkt hoeft dat niet.
   
   Opdracht 60
   Leg uit of het volgende mengsel neutraal is: 1 mol H₂SO₄ + 1 mol NaOH
   
   Opdracht 61
   Leg uit welke van de twee oplossingen de laagste pH heeft en meet, indien mogelijk, de pH:
   1. 1M H₂SO₄ of 1M HCl
   2. 1M HCl of 1M HAc
   3. 0,1M HCl of 1M HAc
   
   
   
   

   6.2 K_w

   In module 9 is al besproken dat water zelf een zwak amfolyt is, dus een zeer zwakke base én een zeer zwak zuur.
   Als er in water geen andere stoffen zijn opgelost, dan is de pH van dat water bij 25 graden precies 7 en ook de pOH = 7.
   Bij het waterevenwicht (H₂O + H₂O H₃O⁺ + OH^-) behoort uiteraard ook een evenwichtsvoorwaaarde K:
   
   
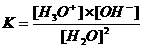
   De waterconcentratie is constant.
   
   Opdracht 62
   Leg uit dat de waterconcentratie ±55,5 mol/l is en dat de watersplitsing daaraan praktisch niets verandert.
   
   
   Uit bovenstaande kan de volgende betrekking worden afgeleid:
   
   K.[H₂O]² = [H₃O⁺].[OH^-] K·55,5 = K_w = 10^-7·10^-7 = 10^-14
   
   Kw noemt men de waterconstante en is bij 25°C : 10^-14
   
   Zoals alle evenwichtsconstanten is ook de waterconstante alleen afhankelijk van de temperatuur.
   
   Opdracht 63
   Meet de pH van gekookt water 1. direkt nadat het heeft gekookt en 2. nadat het weer is afgekoeld.
   
   De bovenstaande formules kun je ook m.b.v. p-waarden opschrijven:
   
   pK_w = pH + pOH
   
   of in getallen:
   
   pK_w = 14 = 7 + 7
   
   Als de pH en de pOH aan elkaar gelijk zijn, dus de [H₃O⁺] en de [OH^-] zijn aan elkaar gelijk, dan is de oplossing neutraal.
   
   Omdat K_w een constante is (dus pK_w ook) moeten pH en pOH samen altijd 14 zijn
   
   bijvoorbeeld: pH = 5 en pOH = 9. [let op: alleen bij kamertemperatuur!]
   
   Als de pH groter wordt, dan wordt de pOH kleiner en v.v.
   
   • Door toevoeging van zuur wordt de [H₃O⁺] groter, dus de pH <.
   • Door toevoeging van base wordt de [OH^-] groter, dus de pOH <.
   
   
   
   

   6.3 K_A en K_B

   Als een zuur(HZ of HA) of een base(Z^- of A^-) in water wordt opgelost, dan stelt zich een evenwicht in.
   HZ is nederlands; HA is engels
   Voor zowel het zuur als voor de base (in water) kan men dan een evenwichtsconstante opstellen:
   
   Omdat de [H₂O] constant is (nl. 55,5 mol/l), wordt deze concentratie ondergebracht bij de evenwichtsconstante K
   
   K_z heet zuurconstante
   K_b heet baseconstante
   
   Opdracht 64
   Bereken de pH van:
   1. 0,1M HAc
   2. 0,1M NH₃
   3. 0,1M HCl
   
   

   Hoe zwakker een zuur, des te kleiner is de zuurconstante Kz. Hoe zwakker een base, des te kleiner is de baseconstante Kb.

   
   (zie hiervoor ook tabel I)
   
   Opdracht 65
   Leg uit waarom sterke zuren en basen in tabel I geen zuur of baseconstante hebben.
   
   Een geconjugeerde base hoort bij een zuur dat één proton heeft afgestaan.
   In tabel I staan geconjugeerde zuren en basen naast elkaar. Het verschil tussen links en rechts is steeds één proton.
   
   Bij 25°C is het product van zuurconstante en baseconstante van de geconjugeerde stoffen altijd 10^-14
   
   Opdracht 66
   Controleer dat in tabel I en bewijs vervolgens dat voor geconjugeerde stoffen altijd geldt: pK_z + pK_b = pK_w(=14)
   
   Slecht oplosbare zouten (dus uit ionen opgebouwd met een stevig ionrooster), waarin een base aanwezig is, zullen pas als base optreden als er een sterk zuur bijgegooid wordt:
   
   Cu(OH)₂(s) + 2HCl(aq) CuCl₂(aq) + 2H₂O
   
   Cu(OH)₂(s) geeft in water geen reactie op een indicator omdat het zo slecht oplosbaar is; de base (de hydroxide-ionen) komt uit zichzelf dan niet vrij.
   
   Opdracht 67
   Leg uit welke pH een mengsel van krijt en water ongeveer zal hebben.
   
   
   • Als je een pH-berekening moet maken, stort je dan niet meteen in de berekening, maar kijk eerst goed om wat voor stof het gaat; welke deeltjes zijn aanwezig? Zijn daar zwakke of sterke zuren of basen bij?
   • Als het bij de berekening om een zure oplossing gaat, reken dan altijd met de pH en/of met de [H₃O⁺].
   • Als het bij de berekening om een basische oplossing gaat, reken dan altijd met de pOH en/of de [OH^-].
   • Zodra je in een formule (bijv. in K_z) een concentratie [...] in moet vullen, dan moet de eenheid mol/l zijn. Zonodig moet je eerst omrekenen.
   
   
   Opdracht 68
   Onderstaande vraagstukken 68a t/m 68d) kunnen eventueel ook als demonstratieproef dienen.
   Ze betreffen het samenvoegen van een bekende hoeveelheid zuur + een bekende hoeveelheid base.
   Je moet natuurlijk eerst weten of en hoe ze met elkaar reageren.
   Zoals altijd bij een chemische reactie zal één van de reactanten op gaan en van de ander zal wat overblijven (tenzij je in staat bent precies de equivalente hoeveelheden samen te voegen).
   De manier waarop je te werk moet gaan is bij elke vraagstuk als volgt:
   1. Zorg er voor dat je precies weet hoeveel zuur er gebruikt wordt
   2. Zorg er voor dat je precies weet hoeveel base er begruikt wordt
   3. Onderzoek m.b.v. een kloppende reactievergelijking welke van de twee op gaat en van welke wat over blijft
   4. Bereken hoeveel er overblijft en reken dit om naar een liter
   5. Hou voortdurend in de gaten met welke volumes je werkt
   
   de vraagstukken:
   1. 0,5 liter 1M H₂SO₄ wordt samengevoegd met 0,5 liter 1M NaOH.
      Bereken de pH van de eindoplossing.
   2. 100 ml 0,05M H₂SO₄ wordt samengevoegd met 100 ml 0,04M kalkwater.
      Bereken de pH voor en na de menging. (25°C)
      Eventueel kan deze proef ook worden uitgevoerd bij 100°C.
   3. 90 ml H₂SO₄ (met pH = 2) wordt vermengd met 10 ml natronloog met (pH = 12). De temperatuur is 25°C.
      Bereken de pH van de verkregen oplossing.
      Eventueel kan deze proef ook worden uitgevoerd bij 100°C.
   4. 50 ml 1M azijnzuur wordt samengevoegd met 50 ml 1M kaliloog.
      Bereken de pH van de eindoplossing.
   
   
   
   

   6.4 Bufferformule

   Opdracht 69
   Bereken eerst de pH van 1M azijnzuur en bereken vervolgens de pH van een mengsel met 1M azijnzuur + 1M natriumacetaat.
   
   Een buffermengsel heeft tot taak de pH van een oplossing zo stabiel mogelijk te houden, ook al wordt er aan die oplossing sterk zuur of sterke base toegevoegd.
   
   In een buffermengsel worden samengevoegd:
   ongeveer evenveel (zwak) zuur (HZ) als geconjugeerde base (Z); die laatste stof kan bijvoorbeeld worden toegevoegd in de vorm van goed oplosbaar NaZ.
   Het HZ heeft tot functie toegevoegde base op te vangen en het Z^- heeft tot functie toegevoegd zuur op te vangen.
   Hoe méér zwak zuur en geconjugeerde base worden samengevoegd, des te méér sterk zuur of base kan worden opgevangen en des te groter is dan de buffercapaciteit.
   
   

   BUFFERMENGSEL: Een tamelijk geconcentreerd mengsel van een zwak zuur met de geconjugeerde base

   
   
   In een oplossing van een zwak zuur geldt altijd:
   [H₃O⁺] = [Z^-] (die twee ontstaan in gelijke mate uit HZ).
   In een buffermengsel echter is veel extra Z^- toegevoegd, zodat in een buffermengsel die twee concentraties niet meer gelijk zijn.
   
   
   1. Als er aan een buffermengsel een beetje sterk zuur wordt toegevoegd, dan wordt dit opgevangen door de aanwezige zwakke base Z^-.
      
      Opdracht 70
      Noteer de reactievergelijking voor de toevoeging een beetje hydroniumion (oxoniumion).
      (De [HZ] wordt iets groter; de [Z^-] wordt dan iets kleiner).
      
   2. Als aan een buffermengsel een beetje sterke base wordt toegevoegd, dan wordt dat opgevangen door het aanwezige zuur HZ.
      
      Opdracht 71
      Noteer de reactie als een beetje OH^- wordt toegevoegd en leg uit wat er dan verandert aan de hoeveelheden HZ en Z^-.
   
   Uit de bekende formule voor Kz (zie onderwerp 18) moet je de zgn. bufferformule kunnen afleiden:
   
   
   nogmaals:
   Nederlandse manier om een zuur aan te geven is vaak: HZ, terwijl in het engels meestal HA wordt gebruikt.
   
   Opdracht 72
   Beantwoord onderstaande drie vragen:
   1. is een mengsel van zoutzuur en keukenzout een buffermengsel? Waarom (niet)?
   2. welke pH heeft een mengsel van 1 mol Natriumoxalaat in 2 liter water?
   3. welke pH heeft een mengsel van 1 mol Natriumoxalaat +1 mol Natriumwaterstofoxalaat in 2 liter water?
   
   
   
   

   6.5 Oplosbaarheidsproduct K_S en oplosbaarheid S

   In tabel XI kun je van een groot aantal stoffen opzoeken of ze oplossen in water (en in andere oplosmiddelen) en zo ja, hoeveel er dan maximaal kan oplossen; dus wanneer ze verzadigd zijn.
   Voor alle stoffen, dus ook voor zouten, is er een verzadigingspunt.
   Slecht oplosbare zouten bereiken dit punt zeer snel, goed oplosbare zouten bereiken dit verzadigingspunt pas veel later.
   
   De oplosbaarheid van een zout wordt meestal aangegeven in de eenheid mol/liter, soms in mol/100 gr.
   
   Als een zout in water (gedeeltelijk) oplost, dan valt het ionrooster (ook gedeeltelijk) uit elkaar; er ontstaan dan meer deeltjes.
   Het oplossen is afhankelijk van de sterkte van het ionrooster, maar ook van de temperatuur. Bij hogere temperatuur valt meer ionrooster uit elkaar.
   
   Opdracht 73
   Verklaar die invloed van de temperatuur.
   
   Slecht oplosbare zouten zijn zouten waarvan het ionrooster slechts voor een (zeer) klein gedeelte uit elkaar valt in water.
   Er is dan sprake van een heterogeen en eenzijdig evenwicht.
   
   Opdracht 74
   Wat wordt bedoeld met een heterogeen en eenzijdig evenwicht.
   Noteer de evenwichtsvergelijking (ook met (s) (l) (g) (aq)) en de evenwichtsvoorwaarde voor de splitsing van zilvercarbonaat in water.
   
   Het kleine beetje zilvercarbonaat dat oplost in water(mol/l) heet de oplosbaarheid S bij een bepaalde temperatuur.
   Let er op dat in dit voorbeeld uit S mol zilvercarbonaat dus gevormd worden: 2S mol zilverionen en S mol carbonaationen.
   De ionen verspreiden zich homogeen door de hele oplossing.
   Omdat het vaste en onopgeloste zilvercarbonaat heterogeen aanwezig is mag voor de concentratie daarvan in de evenwichtsvoorwaarde K de waarde 1 ingevuld worden.
   
   Opdracht 75
   Leg uit dat de evenwichtsconstante K bij deze slecht oplosbare zouten opgevat kan worden als: het ionenproduct in een verzadigde oplossing.
   
   Het ionenproduct (I.P.) in een verzadigde oplossing van een slecht oplosbaar zout noemt men het OPLOSBAARHEIDSPRODUCT K_S
   
   Opdracht 76
   Leg uit of K_s groter of kleiner wordt bij hogere temperatuur.
   
   
   1. Zolang er nog onopgeloste stof op de bodem ligt is de oplossing verzadigd (I.P.= K_s).
   2. Indien dat niet het geval is, dan kan er nog bij en heet het mengsel onverzadigd (I.P.< K_s).
   3. In bijzondere gevallen kan er ook een oververzadigde oplossing worden gemaakt (I.P. > K_s).
   
   Je moet in staat zijn S te berekenen uit Ks en omgekeerd: Ks te berekenen uit S.
   
   Opdracht 77
   Er moet nu geoefend worden met dat omrekenen tussen S en K_s.
   1. Bereken de oplosbaarheid van zilverchloride bij kamertemperatuur in mol/l. [Ks van zilverchloride: 1,5 x 10^-10]
   2. Bereken de oplosbaarheid van zilvercarbonaat bij kamertemperatuur in gr/l. [Ks van zilvercarbonaat: 6 x 10^-12]
   3. Bereken de oplosbaarheid van zilverfosfaat bij kamertemperatuur in mgr/l. [Ks van zilverfosfaat: 2 x 10^-21]
   4. Bereken het oplosbaarheidsproduct van loodchloride in water van 20^oC [S=2 gr/l]
   5. Bereken het oplosbaarheidsproduct van loodchloride in water van 100^oC [S=25 gr/l]
   
   
   
   
   

   ACTIE-OPDRACHTEN

   
   
   Actie-opdracht A: reactieberekeningen
   

   De volgende vier proeven moet je gaan uitvoeren volgens de zes actiepunten van deze leeropdracht:	Noteer steeds, terwijl je bezig bent, alles wat je doet, waarneemt en wat je er bij denkt (chemisch dan natuurlijk) en maak achteraf een overzichtelijk uitgewerkt verslag. Zorg er voor dat je van de te onderzoeken stof steeds voldoende in voorraad houdt. Trek uit elke waarneming steeds voorlopige conclusies, waardoor veel onderzoek overbodig zal blijken te zijn.
   De 4 proeven zijn:	De 6 actiepunten voor elke proef zijn:
   Weeg nauwkeurig ± 0,25 gram onzuiver calcium af en los dit op in een overmaat water (een bijna volle erlemeyer). Het aantal mls gas dat daarbij ontstaat wordt opgevangen en gemeten in een gasmeetspuit. Bepaal de zuiverheid van het calcium in massaprocenten. (Bij kamertemperatuur is het volume van 1 mol gas: 26 liter). Weeg één bruistablet (tegen hoofdpijn e.d.); los deze op in warm water waarvan de totale massa (bekerglas + water) van te voren is gewogen. Dek het bekerglas tijdens de reactie af met een "horlogeglas" en weeg na afloop opnieuw het reactiemengsel. In het bruistablet zitten de stoffen: natriumwaterstofcarbonaat (NaHCO3) en citroenzuur (H3Ci) in de juiste molverhouding, die met elkaar gaan reageren tot ze op zijn. Hoeveel van bovengenoemde stoffen zitten in het bruistablet? Als de rest van het tablet aspirine is, hoeveel aspirine zat dan in zo'n tablet? In kristalsoda (Na2CO3.xH2O) bevindt zich, behalve natriumcarbonaat, ook kristalwater. Weeg nauwkeurig ± 5 gram soda af en los dit op in 50 ml water. Voeg vervolgens ± 5 gram (overmaat) calciumchloride toe; goed roeren en daarna filtreren. Het filter heb je voor de proef gewogen en moet je na de proef opnieuw wegen, maar dan moet het wel eerst gedroogd zijn. Bereken nu hoeveel kristalwater er in soda zit (bereken x). (evtl. i.p.v. III.) Je krijgt een brok koper(II)sulfaat van ongeveer 1 à 2 gram . In dit kristal zit evenals bij soda kristalwater ingebouwd. Stel de formule is CuSO4.xH2O, bereken dan x; bedenk zelf een methode.	Een kloppende reactievergelijking opstellen en de aggregatietoestanden aangeven. Onderstreep de stoffen waarover gegevens bestaan en waarover vragen gesteld worden. De andere stoffen hoef je niet mee te nemen. Die gegevens worden soms direct, soms indirect gegeven. De berekening doe je alleen met de onderstreepte stoffen. Noteer de molverhouding. Als je kans ziet om een proef ook echt uit te voeren, dan doe je dat het beste Waar nodig zet je mol om in de juiste eenheden (zie gegevens en het gevraagde) Voer een omrekeningsfactor in om recht te doen aan de werkelijke hoeveelheden, zoals blijkt uit de gegevens.Zo beëindig je de berekening. Kontroleer / Schat of de uitkomst reëel is, of zo'n uitkomst in werkelijkheid zou kunnen.

   
   
   
   Actie-opdracht B: zuur-base reacties
   

   Voer onderstaande vier proeven uit volgens de vier punten van de leeropdracht:	Noteer steeds, terwijl je bezig bent, alles wat je doet, waarneemt en wat je er bij denkt (chemisch dan natuurlijk) en maak achteraf een overzichtelijk uitgewerkt verslag. Zorg er voor dat je van de te onderzoeken stof steeds voldoende in voorraad houdt. Trek uit elke waarneming steeds voorlopige conclusies, waardoor veel onderzoek overbodig zal blijken te zijn.
   De 4 actiepunten voor elke opdracht zijn:	De 4 proeven zijn:
   Schrijf de formules op van de (opgeloste) stof: [molecuul-,verhoudings-, ionen- en elektronenformules]. Is er een zuur of een base aanwezig? Zo ja, welke? Bewijs dat m.b.v. een indicator. Voer de taak uit. Noteer de waarnemingen. Noteer overzichtelijk alle berekeningen en/of omrekeningen die je hebt gedaan.	Pipetteer 10 ml wijn en verdun deze 10 x m.b.v. een maatcylinder. Bereken hoeveel moleculen alkohol in deze 10 ml zitten en bereken de alkoholconcentratie. Alkohol = ethanol = C2H5OH. Ga uit van het alkoholpercentage op het etiket van de wijnfles. Weeg 1,71 gr suiker af en bereken hoeveel mol en hoeveel moleculen dat is. Los deze suiker homogeen op tot precies 100 ml water (dus in een maatkolf) en bereken de suikerconcentratie. (Suiker = C12H22O11) Stel dat een fles azijn 1M Azijnzuur bevat, hoeveel gram zuur zit er dan in een halve fles? Maak door verdunning ongeveer 0,01M azijnzuur, neem daarvan 10 ml in een erlenmeyer, voeg enkele druppels indicator toe en voeg uit een buret 0,01M NaOH toe tot kleuromslag. Lees af hoeveel ml NaOH werd toegevoegd. Breng precies 10 ml xM HCl in een erlenmeyer; voeg enkele druppels indicator toe. Voeg 0,01M loog toe tot kleuromslag.

   
   
   
   Actie-opdracht C: titraties

   Het is de bedoeling dat je een aantal van de onderstaande titraties samen met je groepje gaat uitvoeren volgens de 10 punten van deze leeropdracht (in de juiste volgorde!):	Noteer steeds, terwijl je bezig bent, alles wat je doet, waarneemt en wat je er bij denkt (chemisch dan natuurlijk) en maak achteraf een overzichtelijk uitgewerkt verslag. Zorg er voor dat je van de te onderzoeken stof steeds voldoende in voorraad houdt. Trek uit elke waarneming steeds voorlopige conclusies, waardoor veel onderzoek overbodig zal blijken te zijn.
   De 10 actiepunten voor elk onderzoek zijn:	De 6 proeven zijn:
   Maak in een ruime tekening duidelijk welke handelingen er achtereenvolgens moeten worden verricht. Zet alle gegevens (formules en rekenkundige gevens) in de tekening bij de betreffende stoffen. Schrijf op met welke stof getitreerd wordt. Welk reactietype vindt plaats bij deze titratie? Hoe kun je het eindpunt bepalen? Leg uit waarom. Schrijf alle reactievergelijkingen op bij de juiste plaats in de tekening. Voer de titratie uit. Was het een direkte of indirekte titratie? Start de berekening bij de molariteit van de titreervloeistof, d.w.z. bereken hoeveel mol van de titreerstof uit de buret werd toegevoegd. Kontroleer wat er precies gevraagd wordt. Voer de rest van de berekening uit en let daarbij op: de juiste molverhouding. verdunningen de juiste eenheden (ml, mol, mmol, mg, l, ml, enz.)	Bepaal door titratie met thio hoeveel gram jodium er is opgelost in een liter trijodideoplossing. Bepaal de azijnzuurconcentratie in azijn door titratie met 0,1M kaliloog. Omdat het azijn te geconcentreerd is moet je eerst die azijn heel precies 10x verdunnen en pipetteer dan 10 ml van die verdunde oplossing. Volgens de warenwet moet er minstens 4 gr azijnzuur in 100 ml azijn zitten; controleer of de onderzochte azijn aan de eis der wet voldoet. Weeg nauwkeurig ongeveer 2,7 gram kristalsoda af: (Na2CO3.xH2O) Voeg daaraan toe enkele druppels methylrood + uit een buret zoveel 1M HCl tot duidelijke kleuromslag naar rood (dit is een overmaat). Verwarm de oplossing even om alle CO2 te verdrijven. Daarna moet je terugtitreren met 0,1M KOH. Gebruik de pHmeter, noteer steeds na bijv. 0,5 ml titreervloeistof de pH en maak een grafiek op grafiekenpapier. Bereken x en ook hoeveel kristalwater er in een halve kilo soda zit. De molariteit van oxaalzuur(aq) kan op twee manieren door titratie worden bepaald: met 0,1M kaliumpermanganaat. Je moet dan ook aanzuren met 1M zwavelzuur en zacht verwarmen bij het begin van de titratie. met 0,1M kaliloog. De ammoniakconcentratie in een schoonmaakmiddel kun je bepalen door titratie met 0,1M HCl, waarbij je het eindpunt bepaalt m.b.v. een geleidbaarheidsmeter. Noteer dan na elke halve ml titreervloeistof de geleidbaarheid van de oplossing en maak een grafiek. Bepaal het vitamine C gehalte van een vitamineC tablet.

   
   
   
   Actie-opdracht D: Buffermengsels

   Volgens de punten I - III moet je met je groepje drie buffermengsels gaan maken en controleren. Daartoe kan gekozen worden uit zes stoffen die in de juiste hoeveelheid moeten worden afgewogen of afgetapt.	Noteer steeds, terwijl je bezig bent, alles wat je doet, waarneemt en wat je er bij denkt (chemisch dan natuurlijk) en maak achteraf een overzichtelijk uitgewerkt verslag. Zorg er voor dat je van de te onderzoeken stof steeds voldoende in voorraad houdt. Trek uit elke waarneming steeds voorlopige conclusies, waardoor veel onderzoek overbodig zal blijken te zijn.
   De 3 actiepunten voor elk onderzoek zijn:	De 6 te gebruiken stoffen zijn:
   Maak het buffermengsel in een volume van ongeveer 100 ml en met een buffercapaciteit van 1 mol/l. Bereken de pH met behulp van de bufferformule en controleer je berekening door die pH te meten met een pHmeter of met pH-papier. Verdeel het buffermengsel in twee delen van ongeveer 50 ml.	Ammoniumchloride azijnzuur ammonia natriummonowaterstoffosfaat natriumacetaat natriumdiwaterstoffosfaat